Clifford Attractors are sequences of 2-dimensional vectors ,
where each new vector N+1 is determined by the preceding vector N, as well as four parameters a, b, c and d, as below.
It can be generalized to higher dimensions, as below. For D dimensions in x, the parameters are (D x D) matrices with suitable values.
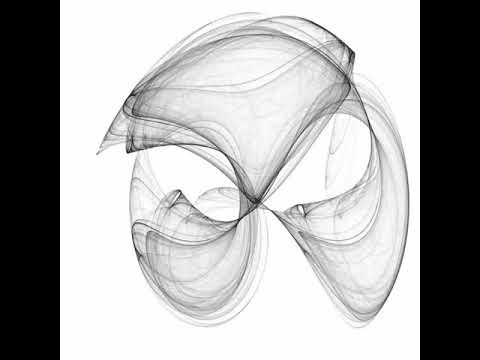
High resolution density plots of such a sequence can be things of beauty, reminiscent of old school screen savers.
Numba translates Python functions to optimized machine code, to drastically quicken calculations and reaching speeds similar to C or Fortran. There are three simple steps when using Numba in python:
- Import just-in-time compilation;
from numba import jit - Add a decorator to the function, e.g.
@jit(nopython=True) - Use only supported variable types and functions
Numba delivers a 4,300% speed improvement, compared to using math trigonometry functions.
This is a remarkable improvement; to achieve the same performance increase through hardware development would
take over a decade, if done according to Moore's law (doubling performance every 2 years).
The improvement compared to a pure NumPy implementation is even more impressive; 18,000%.
| With Numba | Without Numba | |
|---|---|---|
| math trigonometry | 0.224474 | 9.65321 |
| NumPy trigonometry | 0.213497 | 40.35556 |
See timit_clifford_attractors.py for details of the test.
By sampling a large number (tens of billions) of points, we can generate high resolution density plots. Naturally, we use Numba to iterate faster.
Below are example plots, selected after a grid search over the parameter space.
We can animate a 2D attractor, by gradually changing the parameters over time.